Karşılaştırma: Sistem Dinamikleri ve Diferansiyel Denklemler

Geçen yazımda bahsettiğim ödevi buraya aktarmalıyım diye düşündüm. Böylece sistem dinamiklerinin, diferansiyel analize göre sistemlerin dinamiklerini analiz etmede neden daha kolay olduğunu daha güzel gösterebilirim.

Yalnız şimdilik ödevin çözümü hocamızda olduğundan, sadece soru kısmını ve bilgisayardaki kayıtlı kısmını göstereceğim. Kalan kısmı sonraya...

Bir şehirdeki nüfus ve iş yeri miktarı arasındaki etkileşimi konu alıyor ödev. Şehirdeki iş yeri miktarının artışı, müsait arazi miktarına bağlı. Müsait arazi miktarı, toplam şehirdeki arsaların ne kadarının dolduğuna bağlı olarak azalıyor. Yeni iş yerleri oluştukça, arsa miktarı azalıyor. Arsa miktarı azaldıkça da, daha az iş yeri oluşuyor. Bunların arasındaki matematiksel ilişkiler, ödevde verili.

İş yeri sayısının azalması ise, iş yerlerinin ömürlerine bağlı. İnsanlar gibi iş yerlerinin de ömürleri var. Bu da, şehirde yeterince insan bulunmasına bağlı. Bir şehirde, her bir iş pozisyonu için ne kadar çok müsait insan varsa, iş yerlerinin ömürleri o kadar uzun kabul ediliyor. Yeni iş yerleri açıldıkça, toplam iş pozisyonu artıyor. Bu durumda iş pozisyonu başına düşen müsait çalışan sayısı azalıyor. Müsait çalışan sayısı azaldıkça da, iş yerlerinin ömürleri kısalıyor. Bunun sonucunda, daha çok iş yeri kapanıyor.

Bu yukarıda anlattıklarım, iş yerlerinin miktarıyla ilgili sebep sonuç ilişkileriydi. Bunların hepsi ödevde nicel, matematiksel fonksiyonlarla tanımlı.

Bir de nüfus miktarı var. Bir şehirdeki nüfus, net doğumlarla (doğumlardan ölümlerin çıkarılmış hali) artıyor. Net doğum oranını sabit kabul ediyoruz. Dolayısıyla nüfus ne kadar çoksa, o kadar çok doğum oluyor. Bunun sonucunda nüfusun ilelebet artması gerekirdi, fakat nüfus arttıkça, nüfus artışını sınırlayan etkenler hakim hale geliyor. Nedir bunlar? Ödevde sadece bir tanesi ele alınmış:

Nüfus arttıkça, iş arayan kişi sayısı artar. İş arayan kişi sayısı arttıkça, çalışan kişi başına mevcut iş pozisyonu oranı azalır. Çalışan başına iş pozisyonu azaldıkça, o şehirden dışarı doğru göçler artar. Dışarı göçler arttıkça, şehrin nüfusu azalır. Eğer çalışan başına iş pozisyonu çok yüksekse de bu sefer dışarıdan şehre göçler artar. Dolayısıyla göçler hem pozitif hem de negatif etkiye sahip olabilir.

Ödevde ele alınan model bu kadar. Dikkat ederseniz, bu model aslında fiziksel bir mühendislik sistemine ait değil. Bu model, doğrudan sosyal bilimlerin konusuna giren bir alandan alınmış: Bir şehirdeki nüfus ve iş yerlerinin miktarı. Belki ekonomistlerin, kamu yöneticileriin, kent planlayıcılarının veya yerel coğrafyacıların ilgilenebileceği bir sistem.

Şimdi, konuyla ilgilenen sosyal bilimci bir kişi, yukarıdaki sebepsel ilişkilerden çok daha fazlasını muhtemelen biliyordur ve dikkate alıyordur. Fakat sosyal bilimcinin cevap aradığı sorulara, yanıt bulabilmesi için elinde yeterince kolay kullanılabilir, çok güvenilir bir analiz aracı bulunmuyor. En önemli çözümleme aracı herhalde, muhakeme gücü olacaktır. Bu da çok değerli, fakat muhakemeyle ulaşılan sonuçların başka araçlarla da sağlamasının yapılması gerekir.

Sosyal bilimci, eğer matematiğe ilgiliyse, yukarıdaki ilişkileri nicel fonksiyonlarla ifade ettikten sonra, ortaya çıkan diferansiyel denklem sistemini çözerek, sistemin dinamiklerini bulabilir. Fakat sorun şu ki, ortaya çıkan diferansiyel denklem sistemini çözmek gerçek sosyo-ekonomik problemlerde çoğu zaman mümkün değil. Bu ödev olduğundan basit tutuldu, sadece iki tane diferansiyel denklem var. Bu yüzden çözülebiliyor. Ödevi geri aldığımda bunları yazacağım. Şimdi tekrar türetmekle uğraşmaya eriniyorum :)

Fakat sistem dinamikleriyle bu sistemi modellemek ve analiz etmek son derece kolay. İşte size, yukarıda bahsettiğim sistemin (stok-akış) modeli: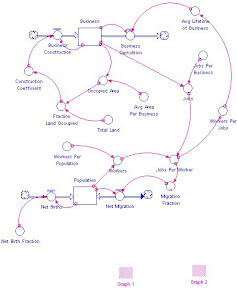



Diyeceksiniz ki, bu muydu kolay dediğin model :) Evet, bu. Çok kolay, hemen gözünüz korkmasın. Şemayı biraz detaylı inceleyin. Anlaşılması çok sezgisel ve kolay. Hiç açıklama yapmıyorum, eminim biraz uğraşsanız, yukarıdaki paragraflarda yazan ilişkilerin, yukarıdaki şemada ifade edildiğini göreceksiniz. Yalnız tabi sebep sonuç ilişkilerinin nicel fonksiyonları bu şemada yok. Onları da aşağıda görebilirsiniz:

Business(t) = Business(t - dt) + (Business_Construction - Business_Demolition) * dt
INIT Business = 105

INFLOWS:
Business_Construction = Business*Construction_Coefficient
OUTFLOWS:
Business_Demolition = Business/Avg_Lifetime_of_Business
Population(t) = Population(t - dt) + (Net_Births + Net_Migration) * dt
INIT Population = 25000

INFLOWS:
Net_Births = Population*Net_Birth_Fraction
Net_Migration = Population*Migration__Fraction
Avg_Area_Per_Business = 5000
Avg_Lifetime_of_Business = 2+12*Workers_Per_Jobs
Construction_Coefficient = 0.1-0.1*Fraction_Land_Occupied
Fraction_Land_Occupied = Occupied_Area/Total_Land
Jobs = Business*Jobs_Per_Business
Jobs_Per_Business = 50
Jobs_Per_Worker = Jobs/Workers
Net_Birth_Fraction = 0.05
Occupied_Area = Business*Avg_Area_Per_Business
Total_Land = 500000
Workers = Population*Workers_Per_Population
Workers_Per_Jobs = 1/Jobs_Per_Worker
Workers_Per_Population = 0.3
Migration__Fraction = GRAPH(Jobs_Per_Worker)
(0.00, -0.1), (0.25, -0.056), (0.5, -0.03), (0.75, -0.012), (1.00, 0.00), (1.25, 0.005), (1.50, 0.008), (1.75, 0.011), (2.00, 0.019), (2.25, 0.029), (2.50, 0.043), (2.75, 0.065), (3.00, 0.1)

Sanırım, inandırıcılığımı yitirmeye başlamış olabilirim :) Bir vaadin daha yanlış çıktığını düşünmeye başlamadığınızı umuyorum. Sevgili arkadaşlar, yukarıdaki denklemler, çok sade denklemler. Tek tek denklemleri okuyun, çok rahat anlaşıldığını göreceksiniz, ki ben hiç açıklama yapmadığım halde. Normalde, bu fonksiyonlarla ifade edilen ilişkilerin anlamı, yazıyla da açıklanır. Fakat ben her zamanki kolaycılığımla, bundan kaçınıyorum :) Bu arada, yine aynı sebeplerden ötürü, terimleri türkçeleştiremediğimden özür dilerim.

Evet, bu yaptıklarımız modellemeyi bitiriyor. Şimdi modelin sonuçlarını görmeliyiz. Simülasyonu çalıştırıyoruz (genellikle Stella, Vensim kullanılıyor, fakat AnyLogic ve Repast gibi yazılımlar da çok iyi). Elde ettiğimiz çok sayıdaki şemadan bir tanesini göstereceğim: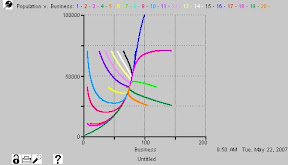



Yukarıdaki şemayı biraz açıklayacağım.

Şimdi yukarıdaki modeli oluşturduktan sonra simülasyonu çalıştırıyorum. Kullandığım yazılım da bana şehirde 100 yıl sonra ne kadar nüfus ve iş yeri olacağını gösteriyor. Fakat doğaldır ki, şehrin 100 yıl sonraki nüfusu ve iş yeri miktarı, bugünkü nüfusuna ve iş yeri miktarına bağlı. Buna başlangıç koşulları (initial conditions) deniyor. Ben de farklı başlangıç koşullarıyla, simülasyonu defalarca çalıştırıyorum. Her birinin sonucunda farklı dinamikler çıkıyor. İşte yukarıdaki şema, yaklaşık 20 farklı denemenin sonuçlarını toplu olarak gösteren şemadır. Yatay eksen, iş yeri miktarını, dikey eksen nüfusu gösteriyor. Şemada farklı renklerle gösterilen her bir eğri, benim her bir simülasyonumdaki evrilmeyi gösteriyor. Yani her bir simülasyonda, zaman içinde, nüfus ve iş yeri miktarları nasıl değişmiş onu gösteriyor.

Dikkat ederseniz, bütün eğriler bir noktada birleşmiş. Bu çok önemli bir sonuç. Bütün sistemlerde böyle olmaz. Bu birleşmenin anlamı şu: yukarıda tanımlanmış olan şehir, başlangıç koşullarından bağımsız olarak, yeterli bir sürenin sonunda, belirli bir nüfus ve iş yeri miktarına gidiyor. Bizim örneğimizde, bu 40000 civarında nüfus ve 80 civarında iş yeri oldu.

Çok ilginç değil mi? Bugün 100 nüfusla da başlasan, 1 milyon nüfusla da başlasan, bu şehrin nüfusu er ya da geç 40 bin olacak diyor, bu analiz.

Şimdilik bu analizden çıkarılabilecek çok sayıdaki bulguyu bir kenara koyalım ve diferansiyel denklemlerin matematiksel analiziyle, simülasyon analizlerinin karşılaştırmasına dönelim. Gördüğünüz gibi, sistem dinamikleriyle bu modeli analiz etmek için, tek yaptığımız modelin unsurları arasındaki ilişkileri basit nicel fonksiyonlarla tanımlamaktan ibaret. Bunun ardından, simülasyon bize sistemin nasıl evrildiğini gösterdi. Peki aynı şeyi matematiksel analizle bulabilir miyiz? Evet, bulabiliriz, zaten bizim ödevin de amacı buydu. Fakat ödev şimdi sevgili hocamızda. Geri döndüğünde, iyi not almışsam :) matematiksel analizi de göstereceğim.

Selamlar sevgiler...

Güncelleme (11.08.2008): Geçtiğimiz günlerde bir Gıda Mühendisliği öğrencisi, ödevin matematiksel çözümünü istemişti benden. Böylece bir sene önce yazdığım bu yazıda verdiğim sözü yeniden hatırlamış oldum. Ödevin resmini çektim ve qipit ile resimleri temizletip pdf'e çevirdim. Dosyayı buradan indirebilirsiniz. 8. sayfadan itibaren, yukarıda bahsettiğim ödevin analitik çözümünü bulabilirsiniz.